[LeetCode Javascript]1 - Two Sum

Problem

Input: an array of integers nums and an integer target.

return indices of the two numbers such that they add up to the target.

Example 1:

Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2:

Input: (nums = [3, 2, 4]), (target = 6);
Output: [1, 2];

Example 3:

Input: (nums = [3, 3]), (target = 6);
Output: [0, 1];

Constraints:

• 2 <= nums.length <= 104
• -109 <= nums[i] <= 109
• -109 <= target <= 109
• Only one valid answer exists

Solution

My Original Solution

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
let twoSum = function (nums, target) {
  const max = nums.length;

  for (let i = 0; i < max; i++) {
    const num1 = nums[i];
    for (let j = i + 1; j < max; j++) {
      const num2 = nums[j];
      if (num1 + num2 === target) {
        return [i, j];
      }
    }
  }
};

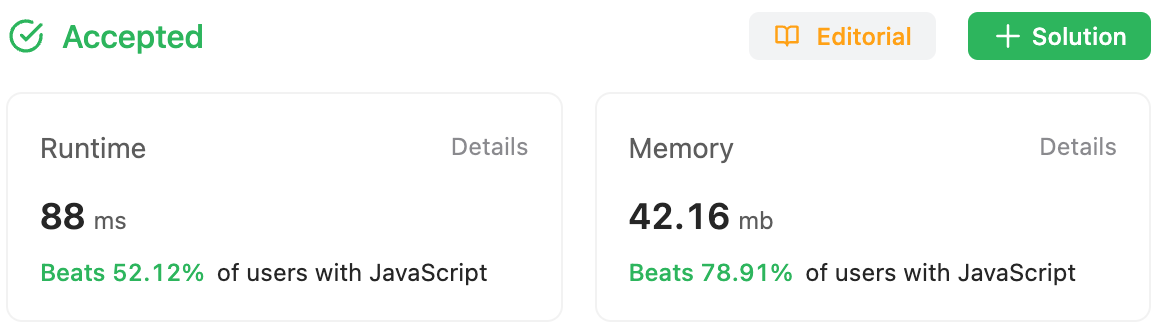
Ok. that’s not good. My code was too slow and needed improvement.

What I learned from this attempt

When I checked the editorial, I informed the expected answer and the problem. They say my approach is Brute Force Approach. Which means it’s so brute. And they can’t see any sign of thought.

They were providing answers in Java and Python. This is the Python code they provide.

Approach 1:Brute Force Algorithm

The brute force approach is simple. Loop through each element xxx and find if there is another value that equals to $target−x$

Complexity Analysis

• Time complexity: $O(n^2)$
• For each element, we try to find its complement by looping through the rest of the array which takes $O(n)$ time. Therefore, the time complexity is $O(n^2)$.
• Space complexity: $O(1)$. The space required does not depend on the size of the input array, so only constant space is used.

Improved Solution

I improved my code as follows, referring to Python and Java answers provided by the editorial description.

The key point is to use ‘Map’ to loop just once.

As the code loops through the ‘nums’ array, it calculates the difference between the current number and the target. If this difference is already present in the Map, it returns the indices of the current number and the mapped value. Otherwise, the current number and its index are stored in the Map for future iterations.

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
let twoSum = function (nums, target) {
  const max = nums.length;
  let map = new Map();

  for (let i = 0; i < nums.length; i++) {
    const num = nums[i];
    const diff = target - num;
    if (map.has(diff)) {
      return [map.get(diff), i];
    } else {
      map.set(num, i);
    }
  }
};

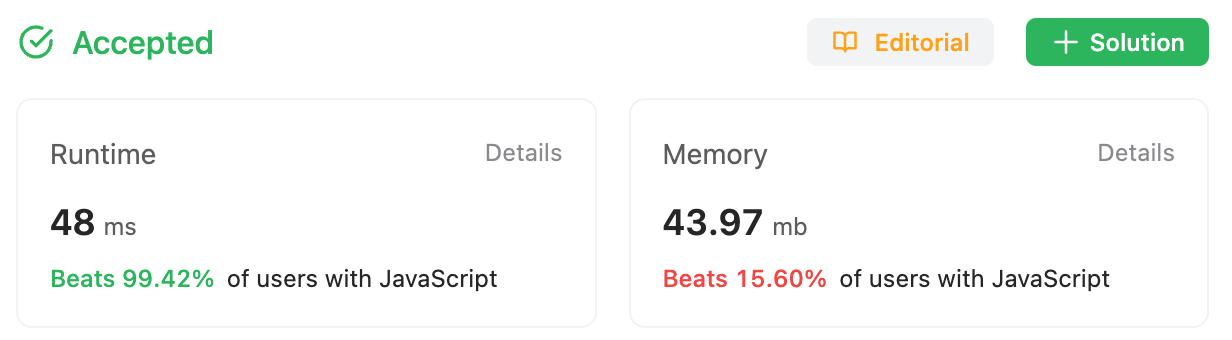
Wow. The revised code shows a significant improvement in runtime—it’s nearly halved. Although there’s a 4% increase in memory usage, the speed enhancement justifies this trade-off.

What I Learned

This is my first time learning about time complexity and space complexity.

Although I was aware of these two concepts in the past, my perspective was rather simplistic – “As long as the code runs, it’s acceptable.”

Now, I realize that this approach can lead to substantial inefficiency in complex projects, causing the unnecessary consumption of resources.

Time Complexity

Definition

The computational complexity that describes the amount of computational time taken by an algorithm to run, as a function of the size of the input to the program. The time complexity of an algorithm quantifies the amount of time taken by an algorithm to run, based on the length of the input. It’s usually expressed using Big O notation, which describes the upper bound of the time complexity in the worst-case scenario.

In this case

I looped through nums. And inside the loop, I looped again. So there is two nested loops in the function.

In the code, the outer loop runs ‘n’ times where ‘n’ is the length of the ‘nums’ array. For each iteration of the outer loop, the inner loop also runs ‘n’ times (technically, it’s less than ‘n’ times because it starts from ‘i + 1’, but when we discuss time complexity, we simplify to the highest order of ‘n’).

So, for each increment in input size, the running time of the algorithm will increase by a factor proportional to the square of ‘n’. This indicates that the algorithm may be inefficient for large input sizes.

In the worst-case scenario, where the target pair is at the end of the array or doesn’t exist, the algorithm will have to iterate through the entire array for each element in the array, resulting in a time complexity of \(O(n^2)\)